1.单分量超导

什么是超导？

首先在一个金属导体中，电子围绕在原子核周围，有许多自由电子在固体的晶格中运动。而超导现象，最常见的就是磁悬浮了，磁悬浮的意思是当给一个固体下方打入磁场，此时固体克服重力漂浮起来，但是在室温下，这种现象不存在，只有在极低温下才会出现，但是为什么这个固体会漂浮，这就是超导理论所解释的了。

超导现象

解释超导现象的理论有两个，其一是BCS理论，其二是GL理论，前者通过微观解释超导现象（从Cooper pair 出发），后者通过宏观的自由能取极小值出发。

BCS理论：

1.固体中的电子：

$$ \psi_\mathbf{k}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_\mathbf{k}(\mathbf{r}) $$

右边的第一项表示由于固体中的周期性边界条件，电子在固体内像自由粒子一样以波矢k沿着晶体运动，而第二项表示电子在固体中一个晶格内（周期）的行为。

电子除了空间分布，还有其自身的运动（自旋s = 1/2），电子可以处于自旋向上或者自旋向下。

固体内有许多处于不同状态的电子（$E_k = \frac{\hbar^2 k ^2}{2m}$），根据Pauli不相容原理：任何的两个电子不能够处于完全相同的量子态（空间+自旋）。

$$ f(E)=\frac{1}{e^{(E-E_F)/k_BT}+1} $$

其中 $E_F$表示电子的Fermi Energy，表示在温度T=0时，电子占据概率为1的最大占据能量，如下图：

因为电子的波矢是一个矢量，并且以相同长度波矢运动的电子处于同一个球面上：

在T等于0时，最大半径的球面就是Fermi面，此时低能级依次全部被占据，当温度升高时，由于热激发，开始有电子从跳跃到更高的能级（上面的f（E）图也能很好的表示这个特征）。

2.Fermi Surface 上的两个电子

两个电子（速度为$v_F \sim10^6\mathrm{~m/s})$）经过费米面，此时费米海已经填满了

首先，两个电子之间有column排斥作用（就好像两个电子之间存在一个弹簧，两个电子靠的很近就会排斥，拉的太远会吸引），它们存在如下的Column作用力：

所以费米面应该是排斥这个电子的，但是由于电子在晶格中运动，晶格由正殿的离子实组成，这当电子1路过的时候，周围的正离子都会靠近这个电子，于是晶格发生了一定的形状变化，导致了局域的正电荷密度增加。

电子2随后经过了这个区域，就被之前电子1吸引的正电荷所吸引，但是由于电子的速度极快，最后看起来电子2被电子1吸引。

有一个形象的比喻：快电子利用笨重的正离子背景做了一个“局部的正电荷陷阱”，并在自己离开后坑了后面来的电子一把。

后果是：两个电子在费米面形成Cooper-Pair，两个电子之间的吸引是由于电子声子耦合超过了两个电子之间的Column 相互作用

3.Cooper-Pair：

Cooper 在1956年证明，在费米海背景下，只要在 Fermi 面附近存在微弱的吸引相互作用，两个电子就能形成能量低于 $2E_F$ 的束缚态（Cooper 对）。

这意味着我们原本认为稳固的费米海基态其实是不稳定的（Cooper Instability）。因为系统总是倾向于处于能量最低的状态，既然形成配对可以降低能量，那么费米面附近的电子就会纷纷两两配对，发生相变。

这种 Cooper 对通常具有以下特征：

动量相反 $(\mathbf{k}, -\mathbf{k})$：为了保证质心动量为零，利用整个费米面的相空间。
自旋相反 $(\uparrow, \downarrow)$：利用单态（Singlet）配对满足交换反对称性。

那么 BCS 理论（1957）在此基础上，进一步计算了在电子电子之间吸引作用下，这个电子气体系统的能谱，并且发现打开了一个Gap。

4.简化模型

$$ V_{\mathbf{k},\mathbf{q}}= \begin{cases} -V & \text{if } E_{F}<\epsilon_{\mathbf{k}}, \epsilon_{\mathbf{q}} < E_{F}+\Delta E \\ 0 & \text{otherwise} \end{cases} \quad(4) $$

上面这个作用势表明，对于两个电子k电子，q电子，而言，当它们的能量处于这个范围内时，感受到的势是-V。

$$ \psi(\mathbf{r_1,r_2})=\sum_\mathbf{k}\left(g_\mathbf{k}e^{i\mathbf{k}(\mathbf{r_1-r_2})}\right)\left(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle\right). $$$$ \psi_{1spatial} = e^{ik_1\cdot r_1} \\\ \psi_{2spatial} = e^{ik_2\cdot r_2} $$$$ \psi_{spatial}(\mathbf{r_1,r_2}) =\psi_{1spatial}\otimes\psi_{2spatial} =\sum_\mathbf{k}\left(g_\mathbf{k}e^{i\mathbf{k}(\mathbf{r_1-r_2})}\right) $$

其中对于所有的波矢线性叠加，表示将所有的动量可能都考虑进去，$g_k$为叠加因子（或者说，现在还不知道Cooper-Pair 的波函数是什么？那么我们先用我们已知的平面波基底对其展开，然后代入薛定谔方程中求解系数）

$$ \left[H_0(\mathbf{r_1})+H_0(\mathbf{r_2})+V(\mathbf{r_1}-\mathbf{r_2})\right]\psi(\mathbf{r_1},\mathbf{r_2})=E\psi(\mathbf{r_1},\mathbf{r_2}) $$$$ H_0(\mathbf{r1}) = \frac{-\hbar^2 \nabla_1^2}{2m} \\ H_0(\mathbf{r2}) = \frac{-\hbar^2 \nabla_2^2}{2m} $$$$ H_0(\mathbf{r1})e^{i\mathbf{k\cdot r_1}} = \frac{\hbar^2 k^2}{2m}e^{i\mathbf{k\cdot r_1}} $$$$ \sum_\mathbf{k}g_\mathbf{k}\left[2\epsilon_\mathbf{k}+V(\mathbf{r_1}-\mathbf{r_2})\right]e^{i\mathbf{k}(\mathbf{r_1}-\mathbf{r_2})}=E\sum_\mathbf{k}g_\mathbf{k}e^{i\mathbf{k}(\mathbf{r_1}-\mathbf{r_2})}. $$

然后两边乘以 $e^{-i\bold{q(r_1-r_2)}}$并对整个空间积分（位置空间）：

可以写为：

BCS理论表明，电子之间的吸引相互作用会导致一种能量更低的Cooper Pair的状态，那么问题是：既然这种吸引相互作用在室温甚至更高温度都存在，或者说这是一种结构上的效果，那么为什么在室温或者其他温度，Cooper-Pair 很难形成？

原因是：在室温下热涨落太剧烈了，在两个电子结合形成Cooper对之后，能量会相比于之前降低一点，但是这个Gap很小，在室温下，环境温度提供能量，导致电子的热涨落太剧烈，使得电子之间的Pair 断开。

Ginzburg - Landau Theory

$$ |\psi(\mathbf{r})|^2 = n_s(\mathbf{r}) $$

当序参量等于0，就说明这个地方没有超导态（SuperConductivity State —SS）只有Normal State（正常态，简称NS）。不等于0说明这里有SS。

GL理论的关键在于，它运用了大自然的懒惰性，即：

大自然是懒惰的，系统将处于自由能最小的状态

$$ F_s=F_n+\underbrace{\alpha|\psi|^2+\frac{\beta}{2}|\psi|^4}_\text{相变势能项}+\underbrace{\frac{1}{2m}|(-i\hbar\nabla-\frac{2eA}{c})\psi|^2}_\text{动能梯度项}+\underbrace{\frac{|H(r)-H_a|^2}{8\pi}}_\text{磁场能} $$

其中Fn代表Normal State的自由能,

相变势能项 $(\alpha|\psi|^2 + \frac{\beta}{2}|\psi|^4)$: 这是描述相变的核心。$\beta$ 是一个正的常数，$\alpha$ 依赖于温度，$\alpha \propto (T - T_c)$：（添加图像解释）

当 $T > T_c$ 时，$\alpha > 0$，能量最低点在 $\psi = 0$（正常态）。
当 $T < T_c$ 时，$\alpha < 0$，能量最低点在 $\psi \neq 0$，导致自发对称性破缺，进入超导态。

动能梯度项存在是为了防止序参量的模方发生巨大的变化（因为自由能是要取最小值的，既然要避免这种情况发生，那么对于优化问题，加上这一项即可）

磁场能量：因为凝聚成超导（形成Cooper-Pair ）会降低系统的自由能（相变势能项），但是形成超导体后需要付出大量抗磁的能量代价，那么II类超导体其实就是在权衡这两点，所以引入了磁通涡旋，两者之间得到了权衡。

需要解释两点：

为什么相变的势能项的幂次是这样的？
动能项为什么多了一个 $\frac{2eA}{c}$

1. 对自由能求极值

对于自由能取极值有两种方式得到两个方程：

$$ \alpha\psi+\beta|\psi|^2\psi+\frac{1}{2m}(-i\hbar\nabla-\frac{2eA}{c})^2\psi=0 $$
$$ j=\frac{2e}{m}\mathrm{Re}\left\{\psi^*(-i\hbar\nabla-\frac{2eA}{c})\psi\right\} $$
（添加对于两个方程的推导）

2. 两个长度

通过上面对于自由能取极值可以得到两个长度，相干长度 $\xi$和渗透长度 $\lambda$

相干长度：

对于一个超导体，假设此时它体内Cooper-Pair的密度均匀，每个地方的序参量相同 $\psi_0$。

此时突然将超导体的边界的序参量变成0（？什么操作），相干长度表示这个操作影响了多少长度的超导体，即表明了这个超导体是软的（相干长度小）还是硬的（相干长度大），如果是软的（像一个具有弹性的物体），它会在表面吸收一定能量，阻止这个影响传播，如果是硬的，那么这个影响就好像波一样向超导体内部传播。

那么如何定义这个相干长度呢？

$$ \frac{-\hbar^2}{2m}\frac{d^2\psi}{dx^2}+\alpha\psi+\beta\psi^3=0 $$$$ \psi_0^2=\frac{-\alpha}{\beta}=\frac{|\alpha|}{\beta} $$$$ \psi(x) = f(x)\psi_0 $$$$ \frac{-\hbar^2}{2m}\psi_0\frac{d^2f}{dx^2}+\alpha(\psi_0f)+\beta(\psi_0f)^3=0 $$$$ -\frac{\hbar^{2}}{2m} \frac{d^{2}f}{dx^{2}} - |\alpha|f + \beta\psi_{0}^{2}f^{3} = 0 $$$$ -\frac{\hbar^{2}}{2m} \frac{d^{2}f}{dx^{2}} - |\alpha|f + |\alpha|f^{3} = 0 $$$$ \frac{\hbar^{2}}{2m|\alpha|} \frac{d^{2}f}{dx^{2}} = f - f^{3} $$

现在请仔细看左边的系数：

系数 $\times \frac{d^{2}f}{dx^{2}}$ = 无量纲数

$\frac{d^{2}f}{dx^{2}}$ 的量纲是 $\frac{1}{长度^{2}}$。
为了让等式两边都无量纲，前面的系数必须具有长度${}^{2}$ 的量纲。

$$ \xi^2(T)=\frac{\hbar^2}{2m|\alpha|} $$$$ \xi^2\frac{d^2f}{dx^2}+f-f^3=0 $$$$ f(x)\approx\tanh\left(\frac{x}{\sqrt{2}\xi}\right) $$

当 x = $\xi$时，序参量恢复到平衡态的66%。

相干长度的正式定义是：描述超导序参量（波函数）受扰动后恢复的距离。

穿透深度：

$$ j=\frac{2e}{m}\mathrm{Re}\left\{\psi^*(-i\hbar\nabla-\frac{2eA}{c})\psi\right\} $$$$ \mathbf{j}= - \frac{4 e^2}{mc}|\psi_0|^2\mathbf{A} $$

根据London 方程，超导体内部形成的电流是与磁场产生的矢势（$\mathbf{B = \nabla \times A}$）成反比的,所以得出超导体是抗磁的，超导电流越大的地方，磁场越小。

自然而然，有一个问题，施加的这个磁场能够在超导体内部穿透多远？

$$ \nabla \times \mathbf{H} = \frac{4\pi}{c}\mathbf{j} $$$$ \nabla \times (\nabla \times \mathbf{H}) = \frac{4\pi}{c}\nabla \times \mathbf{j} $$$$ -\nabla^2\mathbf{H} = - \frac{16\pi e^2}{mc^2}|\psi_0|^2(\nabla \times \mathbf{A})=- \frac{16\pi e^2}{mc^2}|\psi_0|^2\mathbf{H} $$$$ \mathbf{H} = \exp(-\frac{x}{\lambda}),\quad\lambda(T) =\sqrt{\frac{mc^2}{16\pi e^2|\psi_0|^2}} $$$$ \lambda(T) =\sqrt{\frac{mc^2\beta}{16\pi e^2|\alpha|}} $$

穿透深度顾名思义，其越大，磁场越容易穿过超导体，反之亦然。

两类超导体：

$$ \kappa = \frac{\lambda}{\xi} $$

如果 $\kappa > 1/\sqrt{2}$,即为I类超导体，如果小于则为II类超导体。

可以从表面能来理解这种分类。

表面能（Surface Energy）：

$$ E_S = E_C-E_B $$

其中Es表示表面能，Ec代表这个过程中亏损的能量，Eb代表这个过程超导体获得的能量。

分别来看Ec和Eb：

这个过程中亏损的能量是损失了相干长度这么宽的Cooper-Pair的凝聚能。— $\xi \times \text{损失的Cooper 凝聚能}$
获得的能量是带来了穿透深度这么长的磁场能—- $\lambda \times \text{磁场能}$

那么当损失大于收益时，表面能为正，那么此时为I类超导，即此时的相干长度比穿透深度长（为什么？磁场能与Cooper的凝聚能相当。）

损失小于收益时，表面能为负，此时为II类超导，相干长度比穿透深度短。

所以区分I类超导与II类超导的一个角度时，超导体内部磁场能量与Cooper凝聚能量的一个fighting。

I类超导：“比较硬且纯净的超导”，其相干长度大于穿透长度，两败俱伤，因为超导体损失的Cooper能量大于磁场的能量。（比较硬是因为，相干长度长，外部的影响可以传到超导体很深的位置）

II类超导：“比较软且有杂质的超导”，其相干长度短于穿透长度，内部的Cooper对形成了妥协，让磁场穿入超导体（但不是随便穿入磁场，而是以一个磁通涡旋穿入）。要形成II类超导体，可以往超导体内部加入一定量的杂质，这样会使得超导体内部电子的自由程变短（自由程即电子自由运动的一个距离），那么此时超导体的相干长度也会变小，那么此时穿透深度就会大于相干长度了。

上图左边是I类超导，右图是II类超导，I类超导只有一个临界磁场（当磁场超过之后，整个超导态被破环）。II类超导有两个临界磁场，当磁场超过Hc1时超导态转变为混合态（此时允许磁场进入，但是与超导态共存，磁场周围形成许多超导电流屏蔽磁场的影响），当磁场超过Hc2时，与I类超导一样超导态被完全破环。

有一个小问题：根据上面的定义，哪一类超导适合做强磁场下的线圈材料？

磁通涡旋：

II 类超导体表面能为负，让磁场进入超导体，问题是这个磁场如何进入超导体，或者说超导体中的Cooper-Pair 如何与这个磁场相互权衡？

Abrikosov提出了一种磁通涡旋来解释II类超导体中的磁场在超导体中如何穿过。

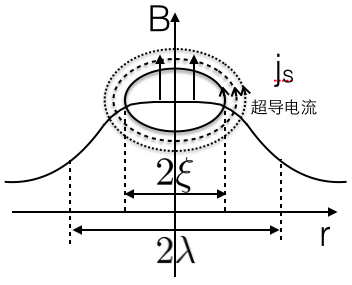
如上图，穿过超导体的磁场，被超导电流环绕在半径为 $\xi$的圆内，但是磁场在离中心 $\lambda$的时候显著减弱，为什么这个超导电流的方向与磁场矢势的方向一样呢？（由London方程，超导电流应该是抵消磁场的！）**首先我们看一个更加普遍的超导电流公式。

$$ \mathbf{j_s}=\frac{2e}{m}\mathrm{Re}\left\{\psi^*(-i\hbar\nabla-\frac{2e\mathbf{A}}{c})\psi\right\} $$$$ \mathbf{j_s}= - \frac{4 e^2}{mc}|\psi_0|^2\mathbf{A} $$$$ \nabla \psi = (\nabla{|\psi|})e^{i\phi} +|\psi|(i\nabla\phi)e^{i\phi} $$$$ \mathrm{Re}\left\{\psi^*(-i\hbar\nabla-\frac{2e\mathbf{A}}{c})\psi\right\} = \\ \mathrm{Re}\left\{-i\hbar |\psi|\nabla{|\psi|}+\hbar|\psi|^2\nabla\phi - \frac{2e\mathbf{A}}{c}|\psi|\right\} $$$$ \mathbf{j_s}= \frac{2e}{m}(\hbar\nabla\phi- \frac{2e\mathbf{A}}{c})|\psi|^2 $$$$ \mathbf{j_s} = n_s (2e) \mathbf{v_s} = |\psi|^2(2e)\mathbf{v_s} $$$$ \mathbf{v_s} =\frac{1}{m}(\hbar\nabla\phi- \frac{2e\mathbf{A}}{c}) $$

那么这个涡旋周围的超导电流有两项，一项是由空间序参量变化导致的（拓扑项），另一项是超导体希望通过反向电流来抵消磁场（抗磁项是London方程所描述的，但是这种情况只适用于Meissner State—完全抗磁态），通过这样一个General的超导电流方程，就可以解释为什么此时超导电流的方向与磁场矢势的方向一致（拓扑项大于抗磁项）。

那么这个涡旋有什么有趣的物理特征呢？—-磁通量子

磁通量子：

$$ \psi(\mathbf{r}) = |\psi(\mathbf{r})| e^{i\phi(\mathbf{r})} $$

这里的 $\phi(\mathbf{r})$ 是相位。

$$ \oint_C \nabla \phi \cdot d\mathbf{l} = 2\pi n, \quad n \in \mathbb{Z} $$$$ \nabla \phi = \frac{m}{\hbar}\mathbf{v}_s + \frac{2e}{\hbar c}\mathbf{A} $$$$ \oint_C \nabla \phi \cdot d\mathbf{l} = \frac{2e}{\hbar c} \oint_C \mathbf{A} \cdot d\mathbf{l} $$$$ \oint_C \mathbf{A} \cdot d\mathbf{l} = \iint_S (\nabla \times \mathbf{A}) \cdot d\mathbf{S} = \iint_S \mathbf{B}\cdot d\mathbf{S} = \Phi $$$$ \Phi = n \left( \frac{2\pi \hbar c}{2e} \right) = n \left( \frac{hc}{2e} \right) = n\Phi_0 $$

其中 $\Phi_0$就成为磁通量子，表明穿过II类超导体的涡旋所携带的磁通量只能是磁通量子的整数倍。